Wykorzystanie ChatGPT do implementacji algorytmu K-średnich w j. python
Przygotowanie pliku z danymi do analizy


Przygotuj zapytanie do ChatGPT
Hej mam tabelę danych w której każdy z rekordów składa się z pól: id produktu, id klienta. Tabela jest zestawieniem zamówień zrealizowanych przez klientów, co oznacza, że każdy rekord informuje co kupił dany klient. Podaj przykład implementacji algorytmu K-średnich w języku Python, który wykorzysta id produktu, id klienta do segmentacji klientów. Jako wynik chciałbym uzyskać plik w którym prócz mich danych pojawi się kolumna z informacją do jakiego klastra został przypisany użytkownika.
Poniższy kod używa biblioteki scikit-learn do implementacji algorytmu K-średnich w Pythonie:
import pandas as pd
from sklearn.cluster import KMeans# Wczytanie danych do Pandas DataFrame
df = pd.read_csv('data.csv')# Wybranie kolumn id produktu i id klienta jako danych wejściowych
X = df[['id_produktu', 'id_klienta']]# Utworzenie obiektu KMeans i ustawienie liczby klastrów na K = 3
kmeans = KMeans(n_clusters=3)# Dopasowanie algorytmu do danych wejściowych
kmeans.fit(X)# Dodanie kolumny z informacją o przypisaniu do klastra
df['klaster'] = kmeans.labels_# Zapisanie wyniku do pliku
df.to_csv('output.csv', index=False)Wynik zapisany zostanie w pliku output.csv z dodatkową kolumną klaster, która informuje do jakiego klastra został przypisany dany użytkownik.
Ponieważ odpowiedź, jaką uzyskałem, nie pozwala ustalić, jaka liczba segmentów klientów dla moich danych będzie optymalna. Zadałem to pytanie ChatGPT.
Jak określić jaka liczba klastrów jest optymalnym rozwiązaniem w segmentacji?
Odpowiedź od AI w moim przypadku wyglądała następująco:
Określenie optymalnej liczby klastrów w algorytmie K-średnich jest trudnym zadaniem i często wymaga interakcji z ekspertem danych lub użycia różnych metod do wyboru.
Niektóre z nich to:
Metoda łokcia (Elbow Method): Polega na wykonaniu wielu iteracji algorytmu K-średnich dla różnej liczby klastrów i zobrazowaniu wyniku na wykresie zmienności średniego dystansu każdego punktu do centroidów klastrów. Optymalna liczba klastrów powinna być tam, gdzie występuje zmiana kąta (łokieć) na wykresie.
Metoda Silhouette: Polega na obliczeniu współczynnika Silhouette dla każdej obserwacji i średniej dla każdego klastra. Współczynnik Silhouette powinien być jak najbliższy 1, co oznacza dobrą separację klastrów.
Metoda gap statistiky: Polega na porównaniu sumy dystansów wewnątrzklastrowych i dystansów międzyklastrowych dla różnych liczb klastrów i wyborze tej liczby, która daje największą różnicę.
Należy pamiętać, że wynik uzyskany przez te metody może być subiektywny i może wymagać dodatkowej analizy lub interpretacji, aby uzyskać optymalną liczbę klastrów.
Zdecydowałem, że na potrzeby optymalizacji mojej eksperymentalnej analizy wybiorę metodę Silhouette. Pozostało mi zadać teraz ostatnie zapytanie do ChatGPT w którym poproszę go o zaktualizowanie kody, tak by uwzględniał metodę Silhouette.
Moje zapytanie wyglądało następująco:
Zmodyfikuj skrypt tak, by program wykorzystał metodę Silhouette do określenia optymalnej liczby klastrów.
Odpowiedź z czatu:
Oto przykład kodu, który wykorzystuje metodę Silhouette do określenia optymalnej liczby klastrów w algorytmie K-średnich w języku Python:
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score# Wczytaj dane z pliku
data = pd.read_csv('data.csv')# Przechowaj dane w tablicy NumPy
X = data[['product_id', 'customer_id']].values# Utwórz pustą listę, aby przechować wyniki współczynników Silhouette
silhouette_scores = []# Petla for dla liczby klastrów od 2 do 10
for n_clusters in range(2, 11):
# Utwórz obiekt KMeans z odpowiednią liczbą klastrów
kmeans = KMeans(n_clusters=n_clusters)
# Dopasuj model do danych
kmeans.fit(X)
# Oblicz współczynnik Silhouette dla bieżącego rozwiązania
silhouette_scores.append(silhouette_score(X, kmeans.labels_))# Znajdź najlepszą liczbę klastrów w oparciu o największą wartość współczynnika Silhouette
best_n_clusters = silhouette_scores.index(max(silhouette_scores)) + 2# Utwórz ostateczny obiekt KMeans z najlepszą liczbą klastrów
final_kmeans = KMeans(n_clusters=best_n_clusters)
# Dopasuj model do danych
final_kmeans.fit(X)# Dodaj kolumnę z informacją o klastrze do oryginalnego zestawu danych
data['cluster'] = final_kmeans.labels_# Zapisz dane do pliku
data.to_csv('segmented_data.csv', index=False)
Dostosowanie skryptu w edytorze kodu Python
Kolejny etap mojej pracy polegał na skopiowaniu kodu z ChatGPT do dowolnego środowiska programistycznego w języku Python. Ja wykorzystałem do tego celu Visual Studio Code, który jest darmowym narzędziem, gdy korzystasz z systemu Windows.
- Wgraj plik z danymi wsadowymi do katalogu, w którym będzie się znajdował program, tak by podmiana nazwy pliku w programie, zapewniła skryptowi dostęp do danych, bez określania dodatkowych ścieżek dostępu.
- Podmieniłem nazwy indeksów w tablicy NumPy na tożsame z moim plikiem wsadowym, czyli id_produktu i id_klienta.
- Dopisałem także 2 linijki kodu, które wyświetlą w terminalu Visual Studio Code wynik Silhouette dla danego klastra i optymalną liczbę klastrów.
#Dodatkowo wyświetlamy informację o wyniku silhouette dla każdego z klastrów
print("Score dla klastrów "+str(n_clusters)+ " wynosi: "+str(silhouette_score(X, kmeans.labels_)))
#Wyświetlamy informację o optymalnej liczbie klastrów
print("Optymalna liczba klastrów: "+str(best_n_clusters))
- pandas;
- scikit-learn – w którego skład wchodzą biblioteki sklearn i gotowe implementacje algorytmu KMeans;
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# Wczytaj dane z pliku
data = pd.read_csv('plik_wsadowy.csv')
# Przechowaj dane w tablicy NumPy
X = data[['id_produktu', 'id_klienta']].values
# Utwórz pustą listę, aby przechować wyniki współczynników Silhouette
silhouette_scores = []
# Petla for dla liczby klastrów od 2 do 10
for n_clusters in range(2, 11):
# Utwórz obiekt KMeans z odpowiednią liczbą klastrów
kmeans = KMeans(n_clusters=n_clusters)
# Dopasuj model do danych
kmeans.fit(X)
# Oblicz współczynnik Silhouette dla bieżącego rozwiązania
silhouette_scores.append(silhouette_score(X, kmeans.labels_))
#Dodatkowo wyświetlamy informację o wyniku silhouette dla każdego z klastrów
print("Score dla klastrów "+str(n_clusters)+ " wynosi: "+str(silhouette_score(X, kmeans.labels_)))
# Znajdź najlepszą liczbę klastrów w oparciu o największą wartość współczynnika Silhouette
best_n_clusters = silhouette_scores.index(max(silhouette_scores)) + 2
#Wyświetlamy informację o optymalnej liczbie klastrów
print("Optymalna liczba klastrów: "+str(best_n_clusters))
# Utwórz ostateczny obiekt KMeans z najlepszą liczbą klastrów
final_kmeans = KMeans(n_clusters=best_n_clusters)
# Dopasuj model do danych
final_kmeans.fit(X)
# Dodaj kolumnę z informacją o klastrze do oryginalnego zestawu danych
data['cluster'] = final_kmeans.labels_
# Zapisz dane do pliku
data.to_csv('segmented_data.csv', index=False)
Spójrzmy na wyniki analizy
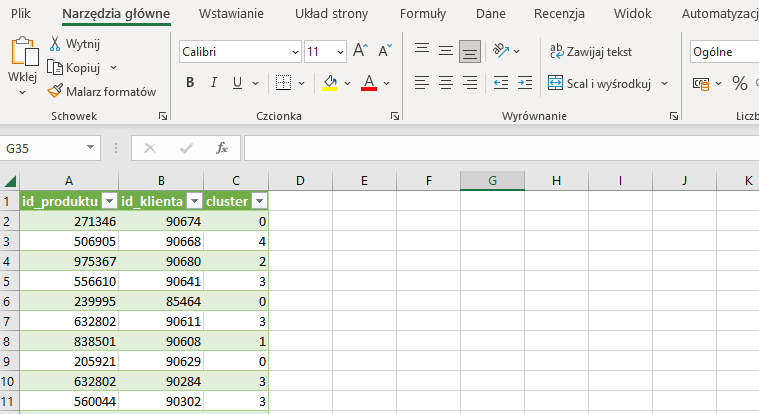
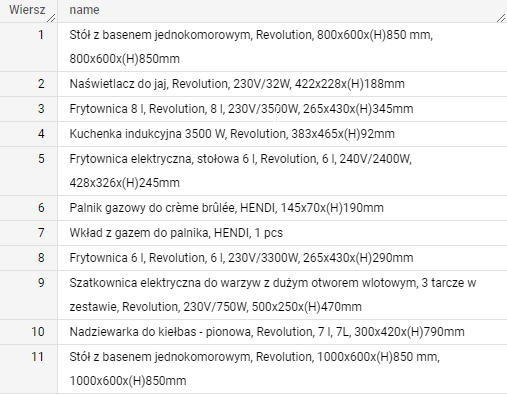
W przypadku klinetów z klastra nr 4, kupowane były m.in.: